Beer is best served cold, and it turns out that math can help with that. Cláudio de Castro Pellegrini of the Federal University of São João del-Rei in Brazil recently set out to formulate an equation to determine the optimal shape of a beer glass that will keep a beverage tastily chilled—in other words, he was looking for a glass that prevents the liquid in it from absorbing heat.
The simplest approach would be to find a vessel whose surface area is as small as possible relative to its volume. That’s because the heat from the glass’s surroundings penetrates the surface of the glass. The smaller this surface is, the less heat gets in, and the longer the beer stays pleasantly cool. As far back as ancient times, scholars recognized that in the case of two dimensions, a circle offers a minimum ratio of circumference to area. And this finding also applies in three dimensions: a sphere has the smallest possible surface area compared with its volume.
But a spherical beer glass would be unwieldy. What’s more, Pellegrini was not interested in a static situation in which you leave beer in a glass and watch the liquid warm up. “The process is quite straightforward here: a request is made for a beer, the waiter delivers it, it is served, it is consumed. Repeat.” he wrote in a preprint paper describing the research, which was posted in October to the server arXiv.org. This means that the level inside the glass changes, and so does the surface that is in contact with the environment. (As more of the glass is drained, more of its surface touches the air around it.)
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Pellegrini started with some constraints on the shape of the glass. It should consist of an insulating, flat base that is large enough to make the glass stand upright. In addition, the glass should be symmetrical so that its shape is represented by a body of revolution, or a three-dimensional shape created by rotating a two-dimensional one 360 degrees around the x axis or y axis. To determine an optimal beer glass shape, Pellegrini adjusted the 2D shape that defines the body of revolution. In an earlier preprint analysis, detailed on arXiv.org in February, he described optimal glass shapes in this way, but the most feasible vessels had a volume of more than two liters—and the largest glass had a volume of more than 100 liters.
Next, Pellegrini aimed to design a realistic beer glass. But he had to make some simplifications. He assumed that the base would insulate heat perfectly. (In reality, a thick glass base and the use of coasters help, but perfect insulation is impossible.) He also assumed that the temperature of the beer would be the same everywhere in the liquid and that the beverage would have a uniform density, which is mostly true for filtered varieties. Pellegrini ignored the beer’s foam as a possible insulating layer. And finally, he also ignored the heat transfer from a person’s hand to the glass, only investigating the effects of the ambient temperature. “In the most critical scenario, such as at the beach on a [38-degree-Celsius] windy day, as few as 3 minutes may be sufficient (again based on personal experience, exhaustively repeated) to render the beer undrinkable,” Pellegrini wrote.
A Formula for the Optimal Beer Glass
With these assumptions, the researcher created an equation that describes the change in temperature of the beer over time. This is a differential equation, meaning the formula contains a derivative: a function that shows the rate of change (of temperature, in this case) with respect to a variable, which in this situation is the beer glass shape:

Here, T is the beer temperature, TU is the ambient temperature, cp is the specific heat capacity (how hard it is to heat up a substance), ρ is the density, V is the volume, Atot is the exposed surface of the beer (including the side and the upper circular surface) and hCV is the convective heat transfer coefficient, representing its ability to conduct heat. Using this formula, Pellegrini calculated four tips to ensure that beer cools down as slowly as possible.
At best, you should enjoy the beer in a cool place so that TU is as low as possible.
If you use a more insulating material such as ceramic instead of glass, the heat conduction coefficient decreases.
In general, Pellegrini pointed out that a thick head of foam insulates the beer and protects it from losing carbon dioxide too quickly. In addition, wind and drafts should be avoided because these lead to forced convection, which plays a much greater role in heat transfer than the natural convection considered here.
All of these tips can usually be followed only by moving to a different location. If you are sitting comfortably in a bar, you are exposed to the local conditions, however, so it would be all the more welcome if, from the outset, bars were to use glasses whose shape was optimized for minimal heat exchange. Spoiler: this is not the case.
The Beer Champagne Flute
The shape of the beer glass is contained in the quotient Atot⁄V in the above equation. The smaller that number, the smaller the temperature change. That’s why Pellegrini focused on minimizing the value of Atot⁄V.
At school, mathematicians learn that such optimization tasks can be solved with derivatives. For example, to find the vertex of a parabola f(x) = x2 + 3x + 2, the function is derived from x and the result is set to zero: 0 = 2x + 3. This means that the vertex can be found at x = –1.5.
Pellegrini proceeded in exactly the same way: He derived the quotient Atot/V, set it to zero and then used the properties of bodies of revolution to derive a function for the optimal shape of a beer glass. According to this, the radius r of a perfect beer glass as a function of the height h is given by the following formula:

C is a constant, and Rb is the radius of the glass base. The formula shows that the mouth opening of the glass should be large, and the glass should become narrower toward the bottom, similar to many common beer glasses. The radius of real-world glasses is not always progressively smaller, however—they often have a curved S shape, as seen from the side. This distinguishes them from a perfect beer glass.
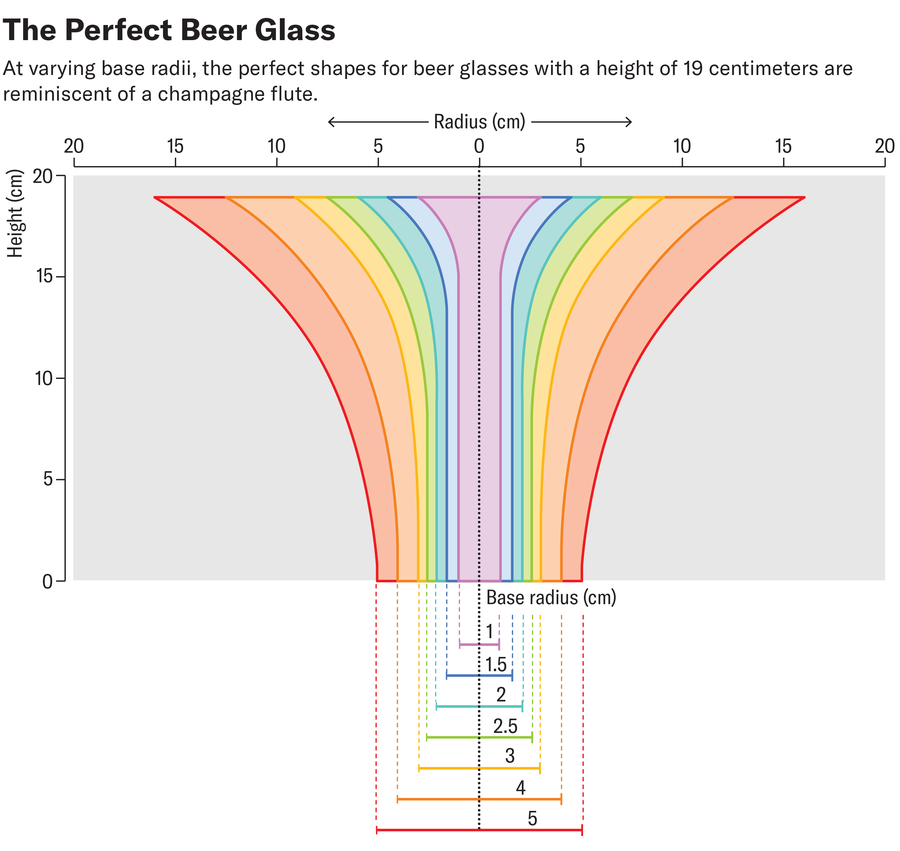
The exact shape of the optimal glass depends on the radius of the glass base and the constant C, which is determined by the height of the glass, among other things. Pellegrini first calculated the optimum shapes for glasses with a height of 19 centimeters for different base radii. The resulting shape is reminiscent of a champagne flute.
The engineer then adapted the parameters of the perfect glass to different types of beer glass, such as the Imperial pint, the American pint or a Weizen (wheat beer) glass, which are widely used in the U.K. To do this, Pellegrini entered the respective base radius and height into his formula to calculate the optimum shape.
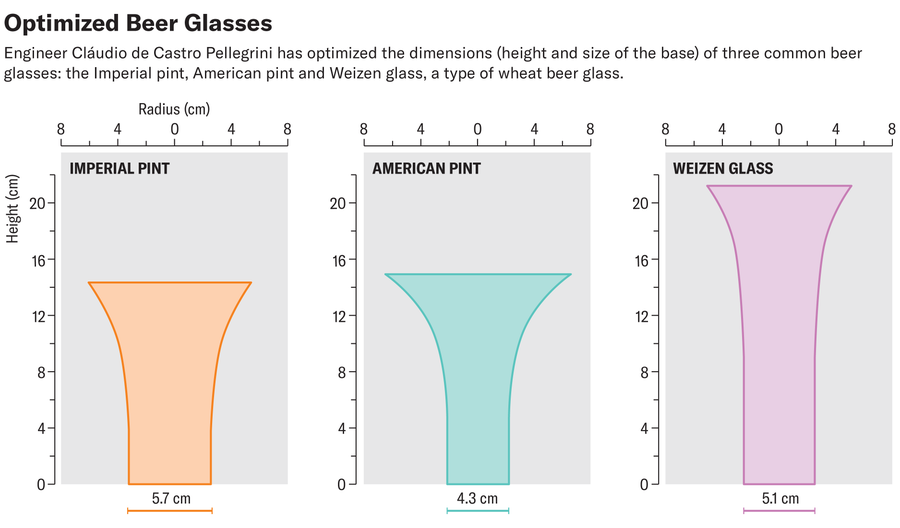
Here, too, the rough shape looks the same for all types and is reminiscent of a champagne flute. But even nonoptimal glasses have some benefits, Pellegrini wrote in the preprint. Although the Nadir Figueiredo glass, which is widespread in Brazil, are far from the optimum shape, they are still perfectly designed for heat transport in certain respects: because they hold a relatively small volume of beer, people usually drink the beer faster than it can warm significantly.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.








